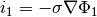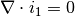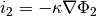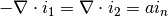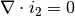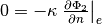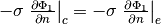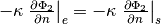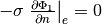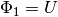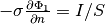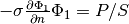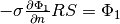Energy storage devices¶
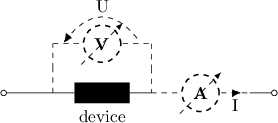
Only the electrical current  and voltage
and voltage  of the device are
measurable. Several operating conditions are possibles. One may want to
impose:
of the device are
measurable. Several operating conditions are possibles. One may want to
impose:
- The voltage
across the device.
- The electrical current
that flows through it.
- The load
the device is subject to.
- The power
.
The class pycap.EnergyStorageDevice is an abstract representation
for an energy storage device. It can evolve in time at various operating
conditions and return the voltage drop across itself and the electrical
current that flows through it.
The rest of this section describes the energy storage devices that are available in Cap, namely:
- Equivalent circuits
- Supercapacitors
Equivalent circuits¶
Series RC¶
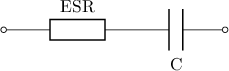
A resistor and a capacitor are connected in series (denoted 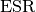 and
and 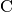 in the figure above).
in the figure above).
type SeriesRC
series_resistance 5.0e-3 ; [ohm]
capacitance 3.0 ; [fahrad]
Above is the database to build a 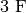 capacitor in series with a
capacitor in series with a
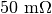 resistance.
resistance.
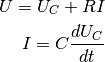
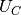 stands for the voltage across the capacitor.
Its capacitance,
stands for the voltage across the capacitor.
Its capacitance, 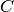 , represents its ability to store electric charge.
The equivalent series resistance,
, represents its ability to store electric charge.
The equivalent series resistance, 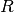 , add a real component to the
impedance of the circuit:
, add a real component to the
impedance of the circuit:
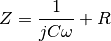
As the frequency goes to infinity, the capacitive impedance approaches zero
and 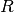 becomes significant.
becomes significant.
Parallel RC¶
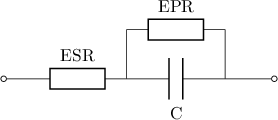
An extra resistance is placed in parallel of the capacitor. It can be instantiated by the following database.
type ParallelRC
parallel_resistance 2.5e+6 ; [ohm]
series_resistance 50.0e-3 ; [ohm]
capacitance 3.0 ; [fahrad]
type has been changed from SeriesRC to ParallelRC.
A 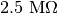 leakage resistance is specified.
leakage resistance is specified.
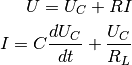
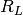 corresponds to the “leakage” resistance in parallel with the
capacitor. Low values of
corresponds to the “leakage” resistance in parallel with the
capacitor. Low values of 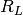 imply high leakage currents which means
the capacitor is not able to hold is charge.
The circuit complex impedance is given by:
imply high leakage currents which means
the capacitor is not able to hold is charge.
The circuit complex impedance is given by:
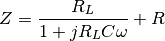
Supercapacitors¶
type is set to SuperCapacitor.
dim is used to select two- or three-dimensional simulations.
device {
type SuperCapacitor
dim 2
geometry {
[...]
}
material_properties {
[...]
}
}
Geometry¶
geometry {
type supercapacitor
anode_collector_thickness 5.0e-4 ; [centimeter]
anode_electrode_thickness 50.0e-4 ; [centimeter]
separator_thickness 25.0e-4 ; [centimeter]
cathode_electrode_thickness 50.0e-4 ; [centimeter]
cathode_collector_thickness 5.0e-4 ; [centimeter]
geometric_area 25.0e-2 ; [square centimeter]
}
The thickness of each layer in the sandwich (anode collector, anode electrode, separator, cathode electrode, cathode current collector) can be adjusted independently from one another. The specified cross-sectional area applies to the whole stack.
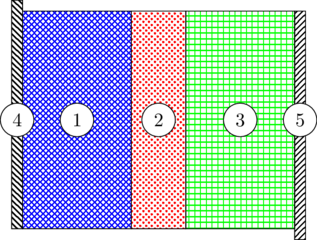
Schematic representation of the supercapacitor conventional sandwich-like configuration. 1: anode electrode, 2: separator, 3: cathode electrode, 4: anode collector, 5: cathode collector.
Governing equations¶
| collector | electrode | separator |
|---|---|---|
|
|
|
| collector-electrode interface | electrode-separator interface |
|---|---|
|
|
| boundary collector tab |
|---|
or
or
or
|
Ignoring the influence of the electrolyte concentration, the current density in the matrix and solution phases can be expressed by Ohm’s law as
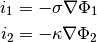
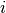 and
and 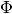 represent current density and potential; subscript
indices
represent current density and potential; subscript
indices 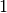 and
and 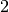 denote respectively the solid and the liquid
phases.
denote respectively the solid and the liquid
phases. 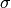 and
and  are the matrix and solution phase
conductivities.
are the matrix and solution phase
conductivities.
The total current density is given by 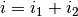 . Conservation of
charge dictates that
. Conservation of
charge dictates that
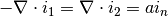
where  is the interfacial area per unit volume and the current
transferred from the matrix phase to the electrolyte
is the interfacial area per unit volume and the current
transferred from the matrix phase to the electrolyte 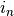 is the sum of
the double-layer the faradaic currents
is the sum of
the double-layer the faradaic currents
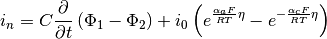
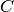 is the double-layer capacitance.
is the double-layer capacitance. 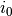 is the exchange current
density,
is the exchange current
density, 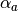 and
and 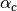 the anodic and cathodic charge
transfer coefficients, respectively.
the anodic and cathodic charge
transfer coefficients, respectively. 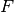 ,
, 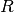 , and
, and 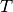 stand
for Faraday’s constant, the universal gas constant and temperature.
stand
for Faraday’s constant, the universal gas constant and temperature.
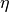 is the overpotential relative to the equilibrium potential
is the overpotential relative to the equilibrium potential
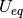
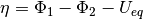
Material properties¶
material_properties {
anode {
type porous_electrode
matrix_phase electrode_material
solution_phase electrolyte
}
cathode {
type porous_electrode
matrix_phase electrode_material
solution_phase electrolyte
}
separator {
type permeable_membrane
matrix_phase separator_material
solution_phase electrolyte
}
collector {
type current_collector
metal_foil collector_material
}
separator_material {
void_volume_fraction 0.6 ;
tortuosity_factor 1.29 ;
pores_characteristic_dimension 1.5e-7 ; [centimeter]
pores_geometry_factor 2.0 ;
mass_density 3.2 ; [gram per cubic centimeter]
heat_capacity 1.2528e3 ; [joule per kilogram kelvin]
thermal_conductivity 0.0019e2 ; [watt per meter kelvin]
}
electrode_material {
differential_capacitance 3.134 ; [microfarad per square centimeter]
exchange_current_density 7.463e-10 ; [ampere per square centimeter]
void_volume_fraction 0.67 ;
tortuosity_factor 2.3 ;
pores_characteristic_dimension 1.5e-7 ; [centimeter]
pores_geometry_factor 2.0 ;
mass_density 2.3 ; [gram per cubic centimeter]
electrical_resistivity 1.92 ; [ohm centimeter]
heat_capacity 0.93e3 ; [joule per kilogram kelvin]
thermal_conductivity 0.0011e2 ; [watt per meter kelvin]
}
collector_material {
mass_density 2.7 ; [gram per cubic centimeter]
electrical_resistivity 28.2e-7 ; [ohm centimeter]
heat_capacity 2.7e3 ; [joule per kilogram kelvin]
thermal_conductivity 237.0 ; [watt per meter kelvin]
}
electrolyte {
mass_density 1.2 ; [gram per cubic centimeter]
electrical_resistivity 1.49e3 ; [ohm centimeter]
heat_capacity 0.0 ; [joule per kilogram kelvin]
thermal_conductivity 0.0 ; [watt per meter kelvin]
}
}
The specific surface area per unit volume  is estimated using
is estimated using
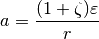
where 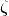 is the pore’s geometry factor (
is the pore’s geometry factor (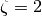 for
spheres,
for
spheres, 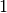 for cylinders, and
for cylinders, and  for slabs) and
for slabs) and  is
the pore’s characteristic dimension.
[M. W. Verbrugge and B. J. Koch, J. Electrochem. Soc., 150, A374 2003]
is
the pore’s characteristic dimension.
[M. W. Verbrugge and B. J. Koch, J. Electrochem. Soc., 150, A374 2003]
The solution electrical conductivity  incorporates the effect
of porosity and tortuosity
incorporates the effect
of porosity and tortuosity
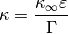
where 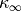 is the liquid phase (free solution) conductivity,
is the liquid phase (free solution) conductivity,
 is the void volume fraction, and
is the void volume fraction, and  is the
tortuosity factor.
is the
tortuosity factor.
The solid phase conductivity is also corrected for porosity (and tortuosity???)
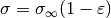
Batteries¶
NOT IMPLEMENTED